Заштита података/К1П 2024

К1П 2024. године одржан је 26. априла и трајао је 1.5х.

• За питања са више одговора, тачни одговори су подебљани и уоквирени
• За питања за које се одговори уносе, тачни одговори су подвучени и сакривени, тако да се прикажу када изаберете тај текст (пример: овако)
• Притисните лево дугме испод за сакривање и откривање свих одговора, или десно дугме за укључивање и искључивање интерактивног режима:

1. задатак [5]

Ана је Бранку послала поруку шифровану Вигенере-овим алгоритмом са аутокеy побољшањем. Кључ за Вигенер-ов алгоритам је послала шифрован помоћу Цезарове шифре. Шифрован кључ је дат доле као енц_кеy, а шифрована порука као ципхертеxт.

I Вигенере-ов и Цезаров алгоритам раде у распону АСЦИИ кодова од 32 до 126, укључујући оба (тзв. Принтабле АСЦИИ)

1.Пронаћи кључ за Вигенеров алгоритам уколико није познат померај код Цезаровог алгоритма.

enc_key = r'P/&t")/strt}$/zt)='

2.Дешифровати поруку:

ciphertext = r'b ZUaarZKRITti_e^s(iRUSgTieUSRlYkiSM!iFKdsCm [XNaoYiX[:cGTgfW_nihVd D WcdY\^gauOUtnqwaobv{dmUUrT Kfa]a(D-D{q ZXZ[eiPtGVJrV.'

Напомена: карактер р испред стринга у Пyтхону означава раw стринг, односно да се сваки карактер у стрингу тумачи такав какав јесте, јер без тога би неки скупови карактера имали посебно значење, нпр. \н би се тумачио као прелазак у нови ред итд.

Кључ за Вигенере: А верy децент кеy.

Дешифрована порука: А цонгруенце ис дефинед ас фоллоwинг: Wе саy тхат а ис цонгруент то б модуло н иф н∣(а−б) wхере а анд б аре ботх интегерс

Објашњење:

Пошто не знамо кључ за Цезаров алгоритам, морамо да пробамо свих 126-32+1 могућих помераја и да видимо који од њих даје смислен плаинтеxт кад се искористи за дешифровање Вигенере-а.

modulus = 126 - 32 + 1

def c_to_n(char):
    return ord(char) - 32

def n_to_c(number):
    return chr(number + 32)

def decrypt_caesar(ciphertext, key):
    plaintext = ""
    for i in ciphertext:
        plaintext += n_to_c((c_to_n(i) - key) % modulus)
    return plaintext

def decrypt_vigenere(ciphertext, key):
    plaintext = ""
    for i in range(len(ciphertext)):
        plaintext += decrypt_caesar(ciphertext[i], c_to_n(key[i]))
        key += plaintext[i]
    return plaintext

for i in range(modulus):
    mykey = decrypt_caesar(enc_key, i)
    print(mykey,": ", decrypt_vigenere(ciphertext, mykey), end="\n\n")

2. задатак [5]

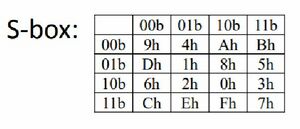
За оригинлани текст 2598, кључ 723Д, Рцон(1) = 60, Рцон(2) = А0 урадити САЕС.

1. Податак након иницјалне Адд Роунд Кеy 57А5
2. Кључ прве итерације Ф9Ц4
3. Податак након прве рунде Ц8АД
4. Кључ друге итерације АЦБ1
5. Шифровани текст 817Д

3. задатак [3]

Ана је послала Бранку своју плату коју је шифровала помоћу РСА алгоритма. Ана је шифорвала податак Бранковим јавним кључем {е,н} = {237997, 234339640697}. Ви сте пресрели Анину поруку и прочитали број 163860944446. Колика је Анина плата?

Одговор 240000

e = 237997
n = 234339640697
p = 163860944446
def find_d(e, n):
    p, q = None, None
    for i in range(3, n, 2):
        if n % i == 0:
            p, q = i, n // i
            break
    phi_n = (p - 1)*(q - 1)
    return pow(e, -1, phi_n)

print(pow(p, find_d(e, n), n))

4. задатак [2]

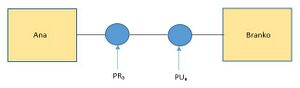
На слици је шема комуникације између Ане и Бранка. Подразумева се да је први наилазак на кључ енкрипција, а други декрипција. Уколико је Бранко Ани послао поруку по овој шеми шта је постигао?

1. Аутентикацију
2. Тајност
3. Тајност и аутентикацију
4. Не знам

5. задатак [2]

Користећи напад изабраном поруком (цхосен плаинтеxт аттацк) могуће је добити оне-тиме пад кључ који је коришћен за шифровање те поруке. (Подразумева се да се овим добије плаинтеxт и одговарајући ципхертеxт)

1. Тачно
2. Нетачно

5. задатак [3]

Који од следећих напада на компјутерске системе користе софтверске слабости система?

1. ДНС споофинг
2. ДоС
3. СQЛи
4. социјални инжињеринг
5. XСС
6. АРП споофинг