АСП2/К1 2014
Први колоквијум 2014. године одржан је 28. октобра 2014.
1. задатак
Поставка
(5п) Нека је дат уређени низ M и секвенца кључева 15, 8, 33, 21, 25 на које се врши претрага. Предложити неопходне структуре података и приказати њихов садржај након симултане претраге задатог низа на више кључева.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 7 | 10 | 11 | 15 | 17 | 20 | 25 | 28 | 29 | 31 | 33 | 36 | 40 |
Решење
Неопходан је додатни вектор за елементе који су већ нађени и њихове индексе. Након симултане претраге задатог низа на више кључева, вектор ће овако изгледати (приметимо да се бројеви 8 и 21 не налазе у низу):
| 15 | 25 | 33 |
|---|---|---|
| 6 | 9 | 13 |
2. задатак
Поставка
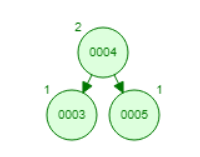
(10п) За стабло бинарног претраживања са слике одредити просечан број приступа приликом успешне претраге и приликом неуспешне претраге, ако је познато да је вредност кључева који се могу уметнути у стабло у опсегу од 1 до 30. Сматрати да су сви кључеви једнако вероватни.
Решење
Из непознатог разлога решење овог задатка је било дато у пдфу са задацима.
| Просечан број приступа приликом успешне претраге: | 36/11=3.28 |
|---|---|
| Просечан број приступа приликом неуспешне претраге: | 62/19=3.26 |
3. задатак
Поставка
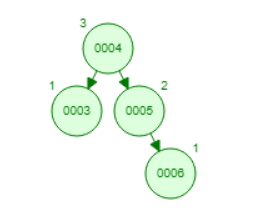
(10п) Приказати по корацима изглед бинарног стабла претраживања са слике, уколико изврши следећа секвенца операција: уметање кључева 19 и 2, а затим брисање кључева 15, 5 и 22. Приликом брисања, користити следбеника.
Решење
4. задатак
Поставка
(10п) У АВЛ стабло се редом умећу кључеви: 5, 3, 4, 6, 12, 9, 7, 16, 18. Приказати, поступно, изглед стабла након сваког уметања кључа.
Решење
5. задатак
Поставка
(15п) Написати у псеудокоду операцију двоструке ротације улево. Нацртати општу слику која објашњава написани псеудокод и на којем су чворови обележени одговарајућим идентификаторима употребљеним у псеудокоду.
Решење
У овом задатку је искоришћено решење из књиге, тј оно што је у књизи названо двоструком ротацијом (две ротације супротног смера, прво лева око левог сина критичног чвора а затим десна око критичног чвора). Две ротације улево око критичног чвора немају смисла.[1]
L-ROT(x) y = x.right temp = y.left y.left = x x.right = temp
R-ROT(x) y = x.left temp = y.right y.right = x x.left = temp
L-DOUBLE-ROT(x) L-ROT(x.left) R-ROT(x)
6. задатак
Поставка
(15п) Написати у псеудокоду и кратко објаснити итеративну имплементацију алгоритма за бинарно претраживање на кључ к, уколико је величина табеле непозната. Сматрати да постоји функција ИН(индеx) која враћа вредност труе уколико задати индекс припада табели, а фалсе у супротном.
Решење
У овом задатку се користи алгоритам за Бинарно претраживање у табели непознате величине из књиге.
EX-SEARCH(L, key)
high=low=1;
if(IN(high)=false) return -1;
if(key = L[1]) return 1;
while(IN(high)=true && key>L[high]) high *= 2;
low = high/2;
while(low<=high)
mid = (low+high)/2;
if(key=L[mid]) return mid;
if(key<L[mid]) high = mid-1;
else low = mid+1;
end_while
return -1;
7. задатак
Поставка
(15п) Објаснити шта је самоподешавајуће стабло, као и мотивацију за ову структуру. Укратко начелно описати операције претраживања, уметања и брисања. Који алгоритам претраживања низова користи сличну стратегију?
Решење
Самоподешавајућа стабла су стабла која одржавају балансираност без неког експлицитног критеријума при уметању и брисању. Уместо тога, реорганизација стабла се врши при сваком приступу стаблу, па и претраживању. Притом се кључеви којима се чешће приступа постављају ближе корену, тако да им се омогући бржи приступ при наредним обраћањима. За ово се користе операције које се заснивају на ротацијама. Мотивација је оптимизација заснована на временској локалности, слично као код транспозиције и пребацивања на почетак код секвенцијалне претраге. Претраживање се врши тако што нађени или последњи не-нулл кључ низом ротација пребацујемо у корен. Уметање се врши тако што прво урадимо претраживање на задати кључ, а ако он не постоји, уметнемо га на одговарајуће место. Брисање се врши тако што се прво врши претраживање на задати кључ, па ако се он пронађе, пребацује се у корен, који се потом брише и мења претходником.
8. задатак
Поставка
(20п) Одговорити на следећа питања у вези оптималног стабла бинарног претраживања. Напомена: Сваки коришћени симбол треба дефинисати и објаснити.
- Прецизно дефинисати оптимално стабло бинарног претраживања за кључеве са вредностима Кн < Кн+1 < ... < Км.
- Ако је кључ Кр корен овог стабла, нацртати општу слику.
- Изразити цену стабла преко цена његових подстабала.
Решење
- Оптимално стабло бинарног претраживања је оно стабло чија је цена најмања, где цену дефинишемо као: , где су Пи вероватноће приступа кључевима Кн...Км, а Qи вероватноће приступа екстерним чворовима.
- .
.
Напомене
- ↑ На К1 2022 је био исти овај задатак и један студент је урадио две ротације улево око x, на шта је Мишић рекао да то нема смисла иако тако пише у задатку.