Заштита података/К1П 2024
K1P 2024. godine održan je 26. aprila i trajao je 1.5h.
- За питања са више одговора, тачни одговори су подебљани и уоквирени
- За питања за које се одговори уносе, тачни одговори су подвучени и сакривени, тако да се прикажу када изаберете тај текст (пример: овако)
- Притисните лево дугме испод за сакривање и откривање свих одговора, или десно дугме за укључивање и искључивање интерактивног режима:
1. zadatak [5]
Ana je Branku poslala poruku šifrovanu Vigenere-ovim algoritmom sa autokey poboljšanjem. Ključ za Vigener-ov algoritam je poslala šifrovan pomoću Cezarove šifre. Šifrovan ključ je dat dole kao enc_key, a šifrovana poruka kao ciphertext.
I Vigenere-ov i Cezarov algoritam rade u rasponu ASCII kodova od 32 do 126, uključujući oba (tzv. Printable ASCII)
1.Pronaći ključ za Vigenerov algoritam ukoliko nije poznat pomeraj kod Cezarovog algoritma.
enc_key = r'P/&t")/strt}$/zt)='
2.Dešifrovati poruku:
ciphertext = r'b ZUaarZKRITti_e^s(iRUSgTieUSRlYkiSM!iFKdsCm [XNaoYiX[:cGTgfW_nihVd D WcdY\^gauOUtnqwaobv{dmUUrT Kfa]a(D-D{q ZXZ[eiPtGVJrV.'
Napomena: karakter r ispred stringa u Pythonu označava raw string, odnosno da se svaki karakter u stringu tumači takav kakav jeste, jer bez toga bi neki skupovi karaktera imali posebno značenje, npr. \n bi se tumačio kao prelazak u novi red itd.
Ključ za Vigenere: A very decent key.
Dešifrovana poruka: A congruence is defined as following: We say that a is congruent to b modulo n if n∣(a−b) where a and b are both integers
Objašnjenje:
modulus = 126 - 32 + 1
def c_to_n(char):
return ord(char) - 32
def n_to_c(number):
return chr(number + 32)
def decrypt_caesar(ciphertext, key):
plaintext = ""
for i in ciphertext:
plaintext += n_to_c((c_to_n(i) - key) % modulus)
return plaintext
def decrypt_vigenere(ciphertext, key):
plaintext = ""
for i in range(len(ciphertext)):
plaintext += decrypt_caesar(ciphertext[i], c_to_n(key[i]))
key += plaintext[i]
return plaintext
for i in range(modulus):
mykey = decrypt_caesar(enc_key, i)
print(mykey,": ", decrypt_vigenere(ciphertext, mykey), end="\n\n")
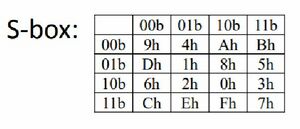
2. zadatak [5]
Za originlani tekst 2598, ključ 723D, Rcon(1) = 60, Rcon(2) = A0 uraditi SAES.
- Podatak nakon inicjalne Add Round Key 57A5
- Ključ prve iteracije F9C4
- Podatak nakon prve runde C8AD
- Ključ druge iteracije ACB1
- Šifrovani tekst 817D
3. zadatak [3]
Ana je poslala Branku svoju platu koju je šifrovala pomoću RSA algoritma. Ana je šiforvala podatak Brankovim javnim ključem {e,n} = {237997, 234339640697}. Vi ste presreli Aninu poruku i pročitali broj 163860944446. Kolika je Anina plata?
Odgovor 240000
e = 237997
n = 234339640697
p = 163860944446
def find_d(e, n):
p, q = None, None
for i in range(3, n, 2):
if n % i == 0:
p, q = i, n // i
break
phi_n = (p - 1)*(q - 1)
return pow(e, -1, phi_n)
print(pow(p, find_d(e, n), n))
4. zadatak [2]
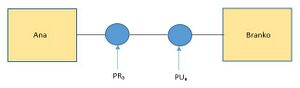
Na slici je šema komunikacije između Ane i Branka. Podrazumeva se da je prvi nailazak na ključ enkripcija, a drugi dekripcija. Ukoliko je Branko Ani poslao poruku po ovoj šemi šta je postigao?
- Autentikaciju
- Tajnost
- Tajnost i autentikaciju
- Ne znam
5. zadatak [2]
Koristeći napad izabranom porukom (chosen plaintext attack) moguće je dobiti one-time pad ključ koji je korišćen za šifrovanje te poruke. (Podrazumeva se da se ovim dobije plaintext i odgovarajući ciphertext)
- Tačno
- Netačno
5. zadatak [3]
Koji od sledećih napada na kompjuterske sisteme koriste softverske slabosti sistema?
- DNS spoofing
- DoS
- SQLi
- socijalni inžinjering
- XSS
- ARP spoofing