Заштита података/К1П 2024

K1P 2024. godine održan je 26. aprila i trajao je 1.5h.

• За питања са више одговора, тачни одговори су подебљани и уоквирени
• За питања за које се одговори уносе, тачни одговори су подвучени и сакривени, тако да се прикажу када изаберете тај текст (пример: овако)
• Притисните лево дугме испод за сакривање и откривање свих одговора, или десно дугме за укључивање и искључивање интерактивног режима:

1. zadatak [5]

Ana je Branku poslala poruku šifrovanu Vigenere-ovim algoritmom sa autokey poboljšanjem. Ključ za Vigener-ov algoritam je poslala šifrovan pomoću Cezarove šifre. Šifrovan ključ je dat dole kao enc_key, a šifrovana poruka kao ciphertext.

I Vigenere-ov i Cezarov algoritam rade sa karakterima iz ASCII tabele sa vrednostima od 32 do 126, uključujući (tzv Printable ASCII)

1.Pronaći ključ za Vigenerov algoritam ukoliko nije poznat pomeraj kod Cezarovog algoritma

enc_key = r'P/&t")/strt}$/zt)='

2.Dešifrovati poruku:

ciphertext = r'b ZUaarZKRITti_e^s(iRUSgTieUSRlYkiSM!iFKdsCm [XNaoYiX[:cGTgfW_nihVd D WcdY\^gauOUtnqwaobv{dmUUrT Kfa]a(D-D{q ZXZ[eiPtGVJrV.'

Napomena: karakter r ispred stringa u Pythonu označava raw string, odnosno da se svaki karakter tumači kao takav, jer bez toga bi skupovi karaktera imali posebno značenje, npr. \n bi se tumačio kao prelazak u novi red itd.

Ključ za Vigenere: A very decent key.

Dešifrovana poruka: A congruence is defined as following: We say that a is congruent to b modulo n if n∣(a−b) where a and b are both integers

Objašnjenje: Pošto ne znamo ključ za Cezarov algoritam, moramo da probamo svih 126-32+1 mogućih pomeraja i da vidimo koji od njih daje smislen plaintext kad se iskoristi za dešifrovanje Vigenere-a.

modulus = 126 - 32 + 1

def c_to_n(char):
    return ord(char) - 32

def n_to_c(number):
    return chr(number + 32)

def decrypt_caesar(ciphertext, key):
    plaintext = ""
    for i in ciphertext:
        plaintext += n_to_c((c_to_n(i) - key) % modulus)
    return plaintext

def decrypt_vigenere(ciphertext, key):
    key = list(key)
    plaintext = ""
    for i in range(len(ciphertext)):
        plaintext += decrypt_caesar(ciphertext[i], c_to_n(key[i]))
        key.append(plaintext[i])
    return plaintext

for i in range(modulus):
    mykey = decrypt_caesar(enc_key, i)
    print(mykey,": ", decrypt_vigenere(ciphertext, mykey), end="\n\n")

2. zadatak [5]

Za originlani tekst 5A8B i ključ 76AE uraditi SAES.

1. Podatak nakon inicjalne Add Round Key
2. Ključ prve iteracije
3. Podatak nakon prve runde
4. Ključ druge iteracije
5. Šifrovani tekst

3. zadatak [3]

Ana je poslala Branku svoju platu koju je šifrovanu pomoću RSA algoritma. Ana je šiforvala podatak svojim javnim ključem {237997, 234339640697}. Vi ste presreli Aniu poruku i pročitali broj 163860944446. Kolika je Anina plata? Odgovor 240000

e = 237997
n = 234339640697
p = 163860944446
def find_d(e, n):
    p, q = None, None
    for i in range(3, n, 2):
        if n % i == 0:
            p, q = i, n // i
            break
    phi_n = (p - 1)*(q - 1)
    return pow(e, -1, phi_n)

print(pow(p, find_d(e, n), n))

4. zadatak [2]

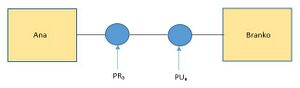
Na slici je šema komunikacije između Ane i Branka. Podrazumeva se da je prvi nailazak na ključ enkripcija, a drugi dekripcija. Ukoliko je Branko Ani poslao poruku po ovoj šemi šta je postigao?

1. Autentikaciju
2. Tajnost
3. Tajnost i autentikaciju
4. Ne znam

5. zadatak [2]

Koristeći napad izabranom porukom (chosen plaintext attack) moguće je dobiti koji ključ je korišćen za one-time pad. (Podrazumeva se da se ovim dobije plaintext i odgovarajući ciphertext)

1. Tačno
2. Netačno

5. zadatak [3]

Koji od sledećih napada na kompjuterske sisteme koriste softverske slabosti sistema?

1. DNS spoofing
2. DoS
3. SQLi
4. socijalni inžinjering
5. XSS
6. ARP spoofing