АСП2/К1 2014 — разлика између измена
(Нова страница: {{tocright}} [https://rti.etf.bg.ac.rs/rti/ri3sp/rokovi/SI2AS2_K1_1415.pdf Zadaci na stranici predmeta.] '''Prvi kolokvijum 2014. godine''' održan je 28. oktobra 2014. == 1. zadatak == === Postavka === '''(5p)''' Neka je dat uređeni niz M i sekvenca ključeva 15, 8, 33, 21, 25 na koje se vrši pretraga. Predložiti neophodne strukture podataka i prikazati njihov sadržaj nakon simultane pretrage zadatog niza na više ključeva. {| class="wikitable" |+ Uređe…) |
м (Замена начина истицања милокода.) |
||
| Ред 94: | Ред 94: | ||
=== Rešenje === | === Rešenje === | ||
U ovom zadatku je iskorišćeno rešenje iz knjige, tj ono što je u knjizi nazvano dvostrukom rotacijom (dve rotacije suprotnog smera, prvo leva oko levog sina kritičnog čvora a zatim desna oko kritičnog čvora). Dve rotacije ulevo oko kritičnog čvora '''nemaju smisla'''.<ref>Na K1 2022 je bio isti ovaj zadatak i jedan student je uradio dve rotacije ulevo oko x, na šta je Mišić rekao da to nema smisla iako tako piše u zadatku.</ref> | U ovom zadatku je iskorišćeno rešenje iz knjige, tj ono što je u knjizi nazvano dvostrukom rotacijom (dve rotacije suprotnog smera, prvo leva oko levog sina kritičnog čvora a zatim desna oko kritičnog čvora). Dve rotacije ulevo oko kritičnog čvora '''nemaju smisla'''.<ref>Na K1 2022 je bio isti ovaj zadatak i jedan student je uradio dve rotacije ulevo oko x, na šta je Mišić rekao da to nema smisla iako tako piše u zadatku.</ref> | ||
< | {{Милокод|<nowiki> | ||
L-ROT(x) | L-ROT(x) | ||
y = x.right | y = x.right | ||
| Ред 100: | Ред 100: | ||
y.left = x | y.left = x | ||
x.right = temp | x.right = temp | ||
</ | </nowiki>}} | ||
< | {{Милокод|<nowiki> | ||
R-ROT(x) | R-ROT(x) | ||
y = x.left | y = x.left | ||
| Ред 108: | Ред 108: | ||
y.right = x | y.right = x | ||
x.left = temp | x.left = temp | ||
</ | </nowiki>}} | ||
< | {{Милокод|<nowiki> | ||
L-DOUBLE-ROT(x) | L-DOUBLE-ROT(x) | ||
L-ROT(x.left) | L-ROT(x.left) | ||
R-ROT(x) | R-ROT(x) | ||
</ | </nowiki>}} | ||
== 6. zadatak == | == 6. zadatak == | ||
| Ред 121: | Ред 121: | ||
=== Rešenje === | === Rešenje === | ||
U ovom zadatku se koristi algoritam za '''Binarno pretraživanje u tabeli nepoznate veličine''' iz knjige. | U ovom zadatku se koristi algoritam za '''Binarno pretraživanje u tabeli nepoznate veličine''' iz knjige. | ||
< | {{Милокод|<nowiki> | ||
EX-SEARCH(L, key) | EX-SEARCH(L, key) | ||
high=low=1; | high=low=1; | ||
| Ред 135: | Ред 135: | ||
end_while | end_while | ||
return -1; | return -1; | ||
</ | </nowiki>}} | ||
== 7. zadatak == | == 7. zadatak == | ||
Тренутна верзија на датум 13. септембар 2024. у 01:09
Prvi kolokvijum 2014. godine održan je 28. oktobra 2014.
1. zadatak
Postavka
(5p) Neka je dat uređeni niz M i sekvenca ključeva 15, 8, 33, 21, 25 na koje se vrši pretraga. Predložiti neophodne strukture podataka i prikazati njihov sadržaj nakon simultane pretrage zadatog niza na više ključeva.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 7 | 10 | 11 | 15 | 17 | 20 | 25 | 28 | 29 | 31 | 33 | 36 | 40 |
Rešenje
Neophodan je dodatni vektor za elemente koji su već nađeni i njihove indekse. Nakon simultane pretrage zadatog niza na više ključeva, vektor će ovako izgledati (primetimo da se brojevi 8 i 21 ne nalaze u nizu):
| 15 | 25 | 33 |
|---|---|---|
| 6 | 9 | 13 |
2. zadatak
Postavka
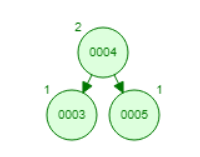
(10p) Za stablo binarnog pretraživanja sa slike odrediti prosečan broj pristupa prilikom uspešne pretrage i prilikom neuspešne pretrage, ako je poznato da je vrednost ključeva koji se mogu umetnuti u stablo u opsegu od 1 do 30. Smatrati da su svi ključevi jednako verovatni.
Rešenje
Iz nepoznatog razloga rešenje ovog zadatka je bilo dato u pdfu sa zadacima.
| Prosečan broj pristupa prilikom uspešne pretrage: | 36/11=3.28 |
|---|---|
| Prosečan broj pristupa prilikom neuspešne pretrage: | 62/19=3.26 |
3. zadatak
Postavka
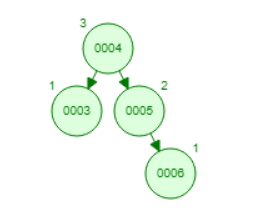
(10p) Prikazati po koracima izgled binarnog stabla pretraživanja sa slike, ukoliko izvrši sledeća sekvenca operacija: umetanje ključeva 19 i 2, a zatim brisanje ključeva 15, 5 i 22. Prilikom brisanja, koristiti sledbenika.
Rešenje
4. zadatak
Postavka
(10p) U AVL stablo se redom umeću ključevi: 5, 3, 4, 6, 12, 9, 7, 16, 18. Prikazati, postupno, izgled stabla nakon svakog umetanja ključa.
Rešenje
5. zadatak
Postavka
(15p) Napisati u pseudokodu operaciju dvostruke rotacije ulevo. Nacrtati opštu sliku koja objašnjava napisani pseudokod i na kojem su čvorovi obeleženi odgovarajućim identifikatorima upotrebljenim u pseudokodu.
Rešenje
U ovom zadatku je iskorišćeno rešenje iz knjige, tj ono što je u knjizi nazvano dvostrukom rotacijom (dve rotacije suprotnog smera, prvo leva oko levog sina kritičnog čvora a zatim desna oko kritičnog čvora). Dve rotacije ulevo oko kritičnog čvora nemaju smisla.[1]
L-ROT(x) y = x.right temp = y.left y.left = x x.right = temp
R-ROT(x) y = x.left temp = y.right y.right = x x.left = temp
L-DOUBLE-ROT(x) L-ROT(x.left) R-ROT(x)
6. zadatak
Postavka
(15p) Napisati u pseudokodu i kratko objasniti iterativnu implementaciju algoritma za binarno pretraživanje na ključ k, ukoliko je veličina tabele nepoznata. Smatrati da postoji funkcija IN(index) koja vraća vrednost true ukoliko zadati indeks pripada tabeli, a false u suprotnom.
Rešenje
U ovom zadatku se koristi algoritam za Binarno pretraživanje u tabeli nepoznate veličine iz knjige.
EX-SEARCH(L, key)
high=low=1;
if(IN(high)=false) return -1;
if(key = L[1]) return 1;
while(IN(high)=true && key>L[high]) high *= 2;
low = high/2;
while(low<=high)
mid = (low+high)/2;
if(key=L[mid]) return mid;
if(key<L[mid]) high = mid-1;
else low = mid+1;
end_while
return -1;
7. zadatak
Postavka
(15p) Objasniti šta je samopodešavajuće stablo, kao i motivaciju za ovu strukturu. Ukratko načelno opisati operacije pretraživanja, umetanja i brisanja. Koji algoritam pretraživanja nizova koristi sličnu strategiju?
Rešenje
Samopodešavajuća stabla su stabla koja održavaju balansiranost bez nekog eksplicitnog kriterijuma pri umetanju i brisanju. Umesto toga, reorganizacija stabla se vrši pri svakom pristupu stablu, pa i pretraživanju. Pritom se ključevi kojima se češće pristupa postavljaju bliže korenu, tako da im se omogući brži pristup pri narednim obraćanjima. Za ovo se koriste operacije koje se zasnivaju na rotacijama. Motivacija je optimizacija zasnovana na vremenskoj lokalnosti, slično kao kod transpozicije i prebacivanja na početak kod sekvencijalne pretrage. Pretraživanje se vrši tako što nađeni ili poslednji ne-null ključ nizom rotacija prebacujemo u koren. Umetanje se vrši tako što prvo uradimo pretraživanje na zadati ključ, a ako on ne postoji, umetnemo ga na odgovarajuće mesto. Brisanje se vrši tako što se prvo vrši pretraživanje na zadati ključ, pa ako se on pronađe, prebacuje se u koren, koji se potom briše i menja prethodnikom.
8. zadatak
Postavka
(20p) Odgovoriti na sledeća pitanja u vezi optimalnog stabla binarnog pretraživanja. Napomena: Svaki korišćeni simbol treba definisati i objasniti.
- Precizno definisati optimalno stablo binarnog pretraživanja za ključeve sa vrednostima Kn < Kn+1 < ... < Km.
- Ako je ključ Kr koren ovog stabla, nacrtati opštu sliku.
- Izraziti cenu stabla preko cena njegovih podstabala.
Rešenje
- Optimalno stablo binarnog pretraživanja je ono stablo čija je cena najmanja, gde cenu definišemo kao: , gde su Pi verovatnoće pristupa ključevima Kn...Km, a Qi verovatnoće pristupa eksternim čvorovima.
- .
.
Napomene
- ↑ Na K1 2022 je bio isti ovaj zadatak i jedan student je uradio dve rotacije ulevo oko x, na šta je Mišić rekao da to nema smisla iako tako piše u zadatku.